Skip to main content

Computational Text Analysis

13 Week 7 Demo

13.1 Setup

First, we’ll load the packages we’ll be using in this week’s brief demo. here we are pre-loading an already-estimated PMI matrix and results from the singular value decomposition approach.

library(Matrix) #for handling matrices
library(tidyverse)
library(irlba) # for SVD
library(umap) # for dimensionality reduction

load("data/wordembed/pmi_svd.RData")
load("data/wordembed/pmi_matrix.RData")

How does it work?

  • Various approaches, including:
      1. SVD
      1. Neural network-based techniques like GloVe and Word2Vec

In both approaches, we are:

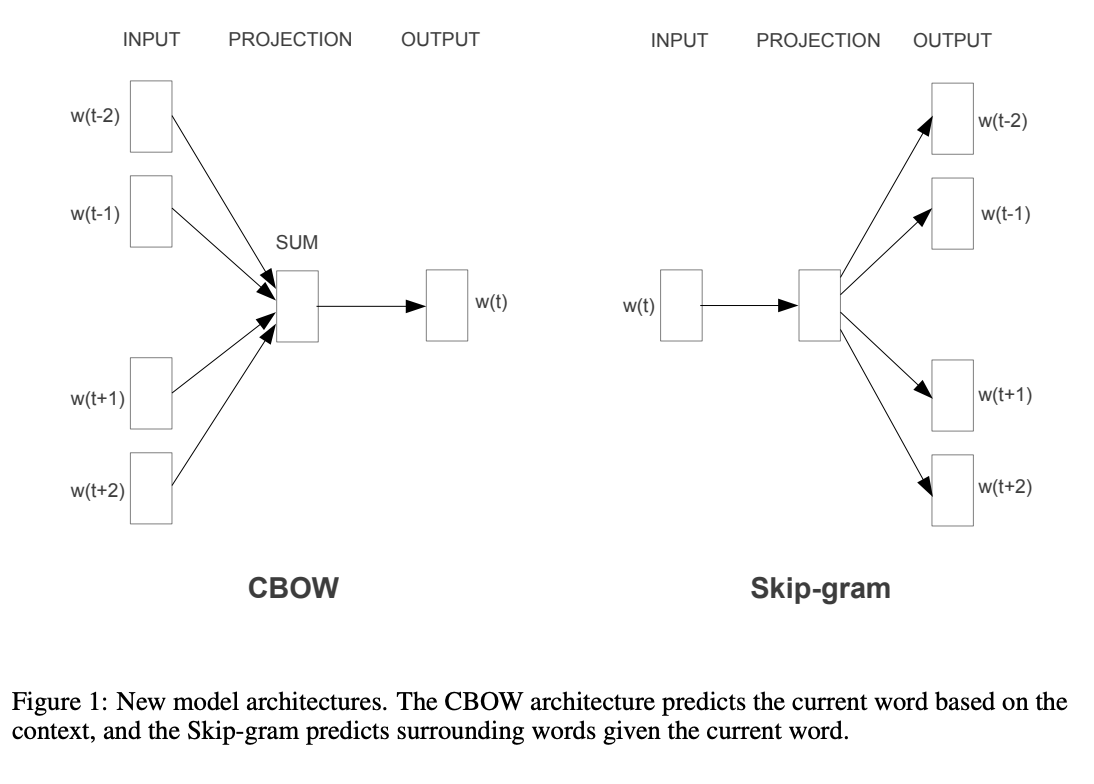
  1. Defining a context window (see figure below)
  2. Looking at probabilities of word appearing near another words
Context window
Context window

The implementation of this technique using the singular value decomposition approach requires the following data structure:

  • Word pair matrix with PMI (Pairwise mutual information)
  • where PMI = log(P(x,y)/P(x)P(y))
  • and P(x,y) is the probability of word x appearing within a six-word window of word y
  • and P(x) is the probability of word x appearing in the whole corpus
  • and P(y) is the probability of word y appearing in the whole corpus
## 6 x 6 sparse Matrix of class "dgCMatrix"
##                the          to          and          of
## the    0.653259169 -0.01948121 -0.006446459  0.27136395
## to    -0.019481205  0.75498084 -0.065170433 -0.25694210
## and   -0.006446459 -0.06517043  1.027782342 -0.03974904
## of     0.271363948 -0.25694210 -0.039749043  1.02111517
## https -0.524615878 -0.57311817 -0.491515918 -0.50450674
## a     -0.325575239 -0.04595798 -0.058629689  0.09829389
##            https           a
## the   -0.5246159 -0.32557524
## to    -0.5731182 -0.04595798
## and   -0.4915159 -0.05862969
## of    -0.5045067  0.09829389
## https  0.5451841 -0.57956404
## a     -0.5795640  1.03048355

And the resulting matrix object will take the following format:

## Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
##   ..@ i       : int [1:350700] 0 1 2 3 4 5 6 7 8 9 ...
##   ..@ p       : int [1:21173] 0 7819 14360 20175 25467 29910 34368 39207 43376 46401 ...
##   ..@ Dim     : int [1:2] 21172 21172
##   ..@ Dimnames:List of 2
##   .. ..$ : chr [1:21172] "the" "to" "and" "of" ...
##   .. ..$ : chr [1:21172] "the" "to" "and" "of" ...
##   ..@ x       : num [1:350700] 0.65326 -0.01948 -0.00645 0.27136 -0.52462 ...
##   ..@ factors : list()

We will then use the “Singular Value Decomposition” (SVD) techique. This is another multidimensional scaling technique, where the first axis of the resulting coordinates captures the most variance, the second the second-most etc…

And to do this, we simply need to do the following.

pmi_svd <- irlba(pmi_matrix, 256, maxit = 500)

After which we can collect our vectors for each word and inspect them.

word_vectors <- pmi_svd$u
rownames(word_vectors) <- rownames(pmi_matrix)
dim(word_vectors)
## [1] 21172   256
head(word_vectors[1:5, 1:5])
##               [,1]        [,2]        [,3]        [,4]
## the    0.007810973  0.07024009  0.06377615  0.03139044
## to     0.006889381 -0.03210269  0.10665925  0.03537632
## and   -0.050498380  0.09131495  0.19658197 -0.08136253
## of    -0.015628371  0.16306386  0.13296127 -0.04087709
## https  0.301718525  0.07658843 -0.01720398  0.26219147
##              [,5]
## the   -0.12362108
## to     0.10104552
## and   -0.01605705
## of    -0.23175976
## https  0.07930941

13.2 Using GloVe or word2vec

The neural network approach is considerably more involved, and the figure below gives an overview picture of the differing algorithmic approaches we might use.